Thursday, April 22, 2010
Wednesday, April 21, 2010
Triangle Congruence
Triangle Congruence Postulates Remember congruent (
) means equal and included means between
Angle-Side-Angle (ASA)
If two angles and the included side of one triangle are congruent to two angles and the included side of the second triangle, then the triangles are congruent.
Side-Side-Side (SSS)
If the three sides of one triangle are congruent to the three sides of a second triangle, then the two triangles are congruent.
- Alll 3 sides are congruent
- ZX = CA (side)
- XY = AB (side)
- YZ = BC (side)
- Therefore, by the Side Side Side postulate, the triangles are congruent.
Side-Angle-Side (SAS)
If two sides and the included angle of one triangle are congruent to the two sides and the included angle of a second triangle, then the two triangles are congruent.
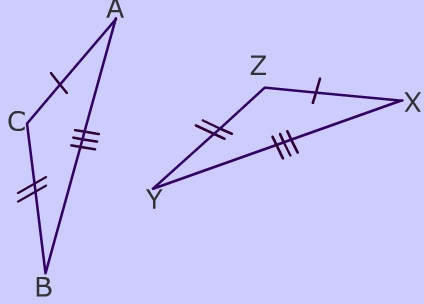
If 
, then the triangles 
are similar.
If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of a second triangle, then the two triangles are congruent.
Example of Angle Angle Side Proof (AAS)
- Two angles and a non-included side are congruent
CAB = ZXY (angle) - ACB = XZY (angle)
- AB = XY (side)
- Therefore, by the Angle Angle Side postulate (AAS), the triangles are congruent.
ABC 
XYZ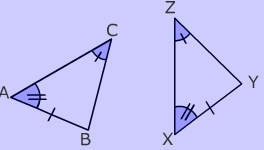 
If the hypotenuse and leg of one triangle are congruent to the hypotenuse and leg of a second triangle, then the two triangles are congruent.
Example 1
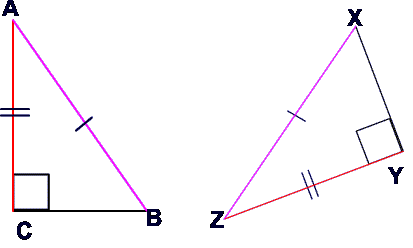
Given AB = XZ, AC = ZY, ACB = ZYX = 90°
Prove ABC XYZ
- ABC and XZY are right triangles since they both have a right angle
- AB = XZ (hypotenuse) reason: given
- AC = ZY (leg) reason: given
- ABC XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent.
Tuesday, April 20, 2010
Chapter 5 Triangles Overview w ans
Chapter 5 Triangles Name __________________
Classifying Triangles by their Angles
Acute Triangles – All angles are less than 90°
Obtuse Triangles – Has an angle greater than 90°
Right Triangles – Has a 90° angle
Equiangular Triangles – All angles are equal(60°) all
Angles are equal, all side lengths are equal.
Classifying Triangles by their Sides
Scalene Triangles – All sides are different lengths.
Isosceles Triangles – At least two sides are congruent (at least two angles will also be congruent)
Equilateral Triangles – All sides are equal lengths.
------------------------------------------------------------------------------------------------------------
In a triangle, the largest angle is across from the __longest______ side of a triangle. List the angles from smallest to largest.
The smallest angle is across (opposite) from the ___shortest____ side of a triangle. List the sides from smallest to largest.
Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side of the triangle.
AB + BC > AC
AC + AB > BC
BC + AC > AB
Exterior Angles of a Triangle
Remote interior angles
A + B + C = 180
C + BCD = 180
The measure of an exterior angle of a triangle is equal to the _measure___ of the measures of the two __remote____ _interior____ ___angles____.
The Exterior Angle Inequality Theorem states that the measure of an exterior angle of a triangle is greater than the measure of either of its remote interior angles.
For more detail information on constructions, see yesterday's post and view the websites listed.
Point of Concurrency
Angle Bisectors of a Triangle- Divides the Angles in half
_Incenter_
Medians of a Triangle - From the vertex to the middle of the ___Centroid______
opposite side
Altitudes of a Triangle – Right angle with the opposite side, ___Orthocenter___
through the vertex
Perpendicular Bisectors of the sides of a Triangle – Bisect the ___Circumcenter___
Sides of the triangle at a right angle
Triangle Congruence Postulates
Angle-Side-Angle
Side-Side-Side
Side-Angle-Side
Angle-Angle-Side
Hypotenuse-Leg
Subscribe to:
Posts (Atom)