Triangle Congruence

Triangle Congruence Postulates                     Remember congruent ( ) means equal and included means between

Angle-Side-Angle (ASA)   

 

If two angles and the included side of one triangle are congruent to two angles and the included side of the second triangle, then the triangles are congruent.

 

 

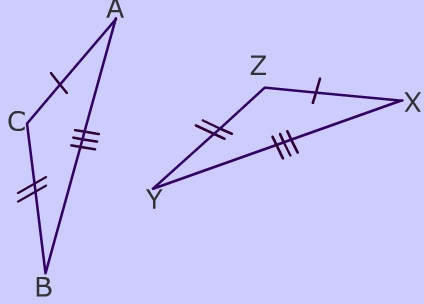
Side-Side-Side (SSS)

If the three sides of one triangle are congruent to the three sides of a second triangle, then the two triangles are congruent.

• Alll 3 sides are congruent
• ZX = CA  (side)
• XY = AB  (side)
• YZ = BC   (side)
• Therefore, by the Side Side Side postulate, the triangles are congruent.

 

 

 

Side-Angle-Side (SAS)

 

If two sides and the included  angle of one triangle are congruent to the two sides and the included angle of a second triangle, then the two triangles are congruent.

 

If , then the triangles are similar.

 

 

Angle-Angle-Side (AAS)

If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of a second triangle, then the two triangles are congruent.

Example of Angle Angle Side Proof (AAS)  

ABC XYZ
• Two angles and a non-included side are congruent
• CAB = ZXY (angle)
• ACB = XZY  (angle)
• AB = XY  (side)
• Therefore, by the Angle Angle Side postulate (AAS), the triangles are congruent.

 

 

Hypotenuse-Leg (HL)

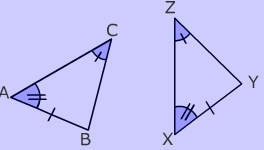
If the hypotenuse and leg of one triangle are congruent to the hypotenuse and leg of a second triangle, then the two triangles are congruent.  

 Example 1  
Given AB = XZ, AC = ZY, ACB = ZYX = 90°
Prove ABC XYZ

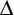• ABC and 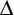XZY are right triangles since they both have a right angle
• AB = XZ (hypotenuse)  reason: given
• AC = ZY (leg) reason: given
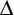• ABC 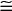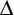XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent.

---