Nored's Notes
Blog Archive
-
▼
2010
(88)
- ► April 25 - May 2 (1)
- ► April 18 - April 25 (6)
- ► April 11 - April 18 (3)
- ► March 28 - April 4 (6)
- ► March 21 - March 28 (2)
- ► March 14 - March 21 (11)
Tuesday, August 31, 2010
Friday, April 30, 2010
4-30 3rd and 4th Block
Distance and Midpoint
The distance formula allows us to find the distance between two points. The formula is a manipulation of the Pythagorean Theorem. Be careful and make sure that the x you use first is the y you use first.
![]()
The midpoint formula allows us to find the middle of a line segment when given the two end points or to find an end point when given the middle and one end.
![]() = midpoint
= midpoint


Thursday, April 22, 2010
Wednesday, April 21, 2010
Triangle Congruence
Angle-Side-Angle (ASA)
If two angles and the included side of one triangle are congruent to two angles and the included side of the second triangle, then the triangles are congruent.

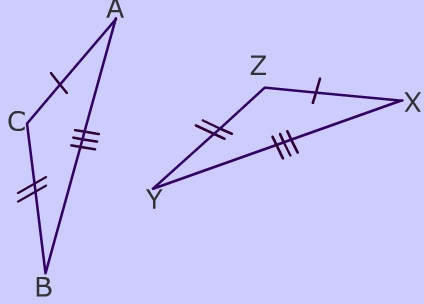
Side-Side-Side (SSS)
If the three sides of one triangle are congruent to the three sides of a second triangle, then the two triangles are congruent.
- Alll 3 sides are congruent
- ZX = CA (side)
- XY = AB (side)
- YZ = BC (side)
- Therefore, by the Side Side Side postulate, the triangles are congruent.
Side-Angle-Side (SAS)
If two sides and the included angle of one triangle are congruent to the two sides and the included angle of a second triangle, then the two triangles are congruent.

If  , then the triangles
, then the triangles  are similar.
are similar.
If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of a second triangle, then the two triangles are congruent.
Example of Angle Angle Side Proof (AAS)
- Two angles and a non-included side are congruent
 CAB =
CAB =  ZXY (angle)
ZXY (angle)  ACB =
ACB =  XZY (angle)
XZY (angle)- AB = XY (side)
- Therefore, by the Angle Angle Side postulate (AAS), the triangles are congruent.
 ABC
ABC  XYZ
XYZ 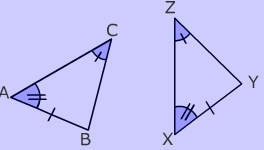
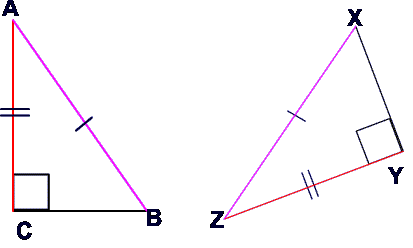
If the hypotenuse and leg of one triangle are congruent to the hypotenuse and leg of a second triangle, then the two triangles are congruent.
Example 1
Given AB = XZ, AC = ZY, ![]() ACB =
ACB = ![]() ZYX = 90°
ZYX = 90°
Prove ![]() ABC
ABC ![]()
![]() XYZ
XYZ
 ABC and
ABC and  XZY are right triangles since they both have a right angle
XZY are right triangles since they both have a right angle- AB = XZ (hypotenuse) reason: given
- AC = ZY (leg) reason: given
 ABC
ABC 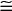
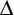 XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent.
XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent.